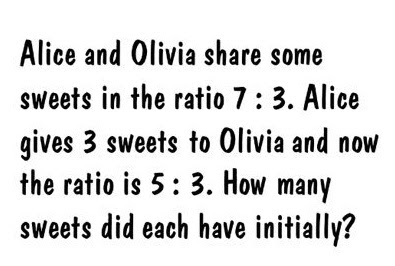New GCSE: Ratio

I've just marked my Year 11 mocks and noticed that ratio continues to be an area of difficulty. This isn't a surprise - we realised a few years ago that ratio questions on the new GCSE are much harder than they used to be. Here's an example of a straightforward ratio question - this is what ratio used to look like at GCSE:

The ratio of boys to girls at a school is 5:7

There are 600 children at the school.

How many boys are there at the school?

But GCSE questions are more challenging now. We're seeing a lot of 'ratio change' questions - this example, from Access Maths, was recently tweeted by Gayle Head (@maths_head):

How would you solve it? Here's an algebraic approach:

I've used equivalent fractions in my workings here - I think this approach really helps my students get the 5 and the 3 in the right place in the equation.

I've seen other teachers use totally different algebraic methods for questions like this (there's a nice example here).

I don't always use algebra for ratio problems - I also teach my students the 'scaling' method. This involves taking the initial ratio and finding a series of equivalent ratios until you find one that works (essentially finding x by trial and error). In this example, we start with 7:3 and multiply by two to get 14:6. Now if Alice started with 14 sweets and Olivia started with 6 sweets, then Alice giving three to Olivia would result in a ratio of 11:9, which is not what we want. So we try again. Our next equivalent ratio is 21:9, and again if we take three from Alice and give them to Olivia we'd get 18:12, which again is not equivalent to 5:3. So we keep going. Our next try is 28:12 which works.

Scaling is sometimes really time consuming. In this example we could have skipped straight to the correct answer if we'd realised that the total number of sweets has to split into 10 parts (ie 7:3) and also into 8 parts (ie 5:3). If we try the lowest common multiple of 10 and 8 then we get the answer really quickly.

We'd use the lowest common multiple if we were going to use bar modelling too.

On the subject of bar modelling - many of us have always drawn bars and boxes on the board when teaching ratio - bar modelling is most definitely not new! However, it is all the rage at the moment and increasingly used in both primaries and secondaries. Over the next few years we'll start seeing many Year 7s coming through to us using bar modelling as a standard approach for many problems, so it is sensible for all secondary teachers to at least know how it works.

If you're not familiar with bar modelling, Kris Boulton's TES article and William Emeny's blog post are a good place to start for the basics. Your local Maths Hub may run a bar modelling course. If you know the basics but struggle with the harder questions, check out this Twitter thread to see a bar model in action for a trickier ratio problem. It's also worth watching this excellent video on solving harder ratio problems using bar models from Colin Hegarty.

Bar modelling certainly is a clear and accessible approach for simple ratio questions. I would say though that for some trickier ratio questions it's not always quite as intuitive and obvious as expert bar modellers suggest it is.

Let's have a look at methods for another 'ratio change' question - this one is from Don Steward:

The algebra method I described above works very quickly. Using equivalent fractions and setting up an equation gives us 8(5x + 2) = 7(6x). The whole solution takes only a few lines of working.

Scaling works too:

5:6 gives 7:6 when Jan gains 2 marbles ✗

10:12 gives 12:12 when Jan gains 2 marbles ✗

15:18 gives 17:18 when Jan gains 2 marbles ✗

20: 24 gives 22:24 when Jan gains 2 marbles ✗

25: 30 gives 27:30 when Jan gains 2 marbles ✗

30: 36 gives 32:36 when Jan gains 2 marbles ✗

35: 42 gives 37:42 when Jan gains 2 marbles ✗

40: 48 gives 42:48 when Jan gains 2 marbles - this simplifies to 7:8 ✓

Again, we can get there more quickly if we think about multiples. We start with a multiple of 11 and end with a multiple of 15, but we gained two marbles along the way. So we can list all multiples of 11 and all multiples of 15 and find a pair which are two apart.

11, 22, 33, 44, 55, 66, 77, 88

15, 30, 45, 60, 75, 90

So we started with 88 marbles.

Not all tricky ratio questions are in the form of these 'ratio change' problems. We also now get GCSE questions like this:

If the ratio a:b is 4:7, write a in terms of b

Though this may seem obvious to many of us (a is the smaller of the two, so a is four sevenths of b), writing the ratios as equivalent fractions can help students get their numbers the right way round (providing they are confident in rearranging equations).

Another type of question is this:

If the ratio a:b is 2:5 and the ratio b:c is 3:10, what is the ratio a:c?

Again, fractions might help.

A quicker alternative is scaling here. We can write a:b:c as one ratio if we get the b parts to match.

a: b can be written as 6:15

b:c can be written as 15:50

So a:b:c is 6:15:50

This shows that the ratio a:c is 6:50, which simplifies to 3:25

And here's another type of question:

Punch is made my mixing orange juice and cranberry juice in the ratio 7:2. Mark has 30 litres of orange juice and 8 litres of cranberry juice. What is the maximum amount of punch that Mark can make?

Again, I think that scaling is probably the quickest approach here. Multiplying the punch ratio by 4 gives us 28:8. This is the most punch we can make because we're using all the cranberry juice. So in total we're making 36 litres of punch.

In summary, there are a variety of approaches for solving trickier ratio problems - most can be solved efficiently using algebra, scaling or bar modelling. If you're teaching this topic for the first time at GCSE it's worth spending some time looking at the various methods. I think our students will need a lot of practice of numerous different types of ratio question to prepare for their GCSE.


Resources
I've created a lesson to accompany this post - download it from TES here.

Here are some other resources that you might find helpful:

• Mel from JustMaths collated ratio Higher GCSE questions from sample and specimen papers here, and has written up her solutions here. 
• If you subscribe to MathsPad then you'll be pleased to hear that they have lovely resources for ratio including a set of questions for Higher GCSE with loads of examples like the problems I've featured in this post.  
• Don Steward has plenty of ratio tasks including his set of 'Harder Ratio Questions' and a really helpful collection of GCSE ratio and proportion questions.
• On MathsBot you can generate ratio questions, revision grids and practice papers. Select 'ratio, proportion and rates of change' at the top.
• There are exam style questions in this collection from Lucy Kilgariff on TES.
• OCR has a 'Calculations with Ratio' Topic Check In and AQA has a Ratio and Proportion Topic Test.
• David Morse of Maths4Everyone has shared a set of revision exercises and ratio exam style questions.

There are loads more ratio resources in my number resources library.

I hope this post will be helpful when you teach ratio at GCSE. Do tweet me to let me know what methods you use if I haven't mentioned them here.

Jo's Blog Posts in 2017

I wrote 55 blog posts in 2017 - just over one per week - which is far fewer than the 78 posts I published in 2016. This wasn't intentional. My new job is pretty full on and since September it's been hard to find the time to write. This is frustrating because I love blogging!

Every December I like to reflect on what I've written about over the course of the year. Today I'm featuring a selection of the posts I particularly enjoyed writing - just in case you missed them.

Dan Walker
I loved writing a post about Dan Walker's Resources back in February because I got to spend time looking through all his lovely PowerPoints. It ended up being one of my favourite posts of the year. If you're not familiar with these fantastic resources then have a look now!

Challenging Algebra
My recent post 'Algebraic Fluency - 50s Style' generated a lot of interest and enthusiasm. A number of teachers emailed me to say that this post led to discussions in their maths department about how we can increase the level of challenge in the algebra questions we give to our GCSE students. This post also initiated a collaborative project to get some of the exercises typed up - I will blog about this over Christmas.

National Challenges and Competitions

When I joined the teaching profession I was surprised that there appeared to be no central source of information - many things were communicated by word of mouth or through local authority networks, and some schools knew very little about what was available nationally to support teachers and students. Over the years I have attempted to fix this by publishing 'listings' - conference dates, school trips, in-school enrichment, and so on. The most recent addition to this catalogue of information is my post about maths challenges and competitions. I hope that by publishing this post, more students will be given access to these fantastic opportunities.

Source: Primary Maths Challenge

What's Happening In My Classroom

I like to write about things that I do in my classroom - it's a good opportunity for me to reflect and improve. There used to be lots of maths bloggers who did this, but it's increasingly rare. I'd love to read more about what goes on in other schools. My post about Papers Society and Structured Revision Lessons gave teachers an insight into what I was doing with my Year 11s in the run up to their GCSE exams, and my post The Folder Experiment... Revisited described why my students now use folders instead of exercises books. In my post Working Well: C1 and C2 I wrote about some things I was trying with my Year 12s including vertical binomial expansions and the grid method for division.

Cover Work
In Cover Work I shared a standard template for a cover lesson in maths - one that I ended up using many times in setting work for a supply teacher over the last few weeks. I hope that other teachers have found this template useful too.

September Lessons

I don't like all my posts to be about resources - sometimes I have opinions to share too! - but I know that maths teachers benefit most when I share resources that save them time. In my post Bridging the Gap... Revisited I wrote about the transition from GCSE to A level and shared a simple algebra test for assessing students at the start of Year 12. In Planning for September: Year 12 I shared some ideas and resources for the first week of term.

New GCSE Topics
To conclude my series of posts looking at new GCSE topics, I wrote New GCSE: Functions in which I explained the new GCSE specification for functions and shared some helpful resources for this topic. With over 6,000 visits so far it's the most viewed post I wrote in 2017. I guess people use it when they're planning their functions lessons. This makes me happy.

Surprisingly, my most viewed post of all time is still - after three years - my post about methods for finding a Highest Common Factor and Lowest Common Multiple, which has had almost 30,000 views. It's worth a read if you're teaching this topic - Venns are not your only option here.
 

I hope you found my blog posts helpful in 2017. Do check out my archive for the full collection of posts and my list of maths gems for all the latest resources and updates.

New this Christmas

I have a page of seasonal resources which includes Christmas-themed maths activities. I think it's really important to do mathematics in every maths lesson throughout the year, but if half the class are out at carol service rehearsals or a lesson is cut short by an end of term assembly, then I see no harm in putting on a bit of Christmas background music while students get stuck into some festive algebra. I love a bit of Wham with my equations.

There are some classics on my seasonal resources page, such as Chris Smith's much-loved relay, but also quite a lot of new additions this year. I thought it might be helpful to list a few of these new resources here so you don't miss anything.

Topic Based
Dave (@d_e_humpty) has produced a lovely set of Christmas shape transformation activities which include translations, reflections and rotations.

Grant (@AccessMaths) has been hard at work producing Christmas resources including a Bauble Puzzle and a Higher and Foundation Christmas Tree Algebra Puzzle. 

MyMaths also has a new collection of Christmas resources including Christmas Algebra which might be suitable for Key Stage 2. 

Mr Bayle (@mrbaylemaths) shared a quick Christmas data collection activity where you play Jingle Bell Rock and students keep a tally of the word count for 'Jingle', 'Bell' and 'Rock'. 

Students at @Maths_CCB had a go, and made festive pie charts of the results.

Danielle (@PixiMaths) has helpfully shared a mixed-topic maths quiz that she made for her Year 9s.

Enrichment 
It's nice to veer off-syllabus for a lesson or two. La Salle have a selection of Christmas enrichment resources including How to make an origami Santa and Christmas Colours which relates to the Four Colour Theorem.

Hexaflexagons are a personal favourite of mine. I became addicted last year after watching Vi Harts's outstanding hexaflexagon videos (if you haven't watched these yet, please do!).

I ran a couple of hexaflexagon lessons in the last week of the summer term. I showed the Vi Hart videos then handed out some templates for colouring. The videos got my students suitably excited about making hexaflexagons but some of them spent absolutely ages colouring, and then for the last 15 minutes of the lesson I had 30 hands up wanting help with the folding and flexing! Hard work. Most students ended up leaving the lesson with both a working hexaflexagon and cool mathematical stories to share at home.

Thanks to Jo Tomalin for sharing a festive hexaflexagon design.

Holiday Work

If your Year 11s have mocks in January then you might want to set them some Christmas holiday homework. Mel (@Just_Maths) has created lovely holiday GCSE homeworks for both Foundation and Higher tier. She has also shared a similar holiday homework for Key Stage 2.

Form Time

If you have any extended form time on the last day of term and your school hasn't provided any resources to keep your students entertained, try Mel's (@Just_Maths) excellent Christmas Pub Quiz.

Alternatively, maths teacher Graham Coleman (@colmanweb) has updated his awesome website Guess the Tunes which now includes Guess the Lyrics and Guess the Faces.

Cards and Gifts 

Maths Ed (@MathsEdIdeas) has shared a Christmaths card for schools to distribute to students and families, encouraging shared maths-play over the holidays. Editable files can be downloaded here and printed onto A4 to fold to A5. 

Finally, do check out my post The Top 5 Christmas Presents for Maths Teachers if you still have some Christmas shopping to do.

Enjoy the last week of term! The end is in sight.

Teachers Wine Glass from notonthehighstreet.com

Algebraic Fluency - 50s Style

Whilst visiting the Mathematical Association in Leicester on Saturday, I picked up a couple of old maths textbooks from the 1950s. 'A Classbook of Algebra' is my favourite.

In it I found some wonderful exercises for developing algebraic fluency, including this set of questions on 'Miscellaneous Factors':

The instruction 'factorise where possible' adds a delightful extra level of intrigue and challenge to this exercise. I love these questions...

Factorise c - 3 + 2x(3 - c)

Factorise c² - (c - d)²

Factorise ef - 1 + e - f

Factorise -14yz + y² + 49z²

Factorise 81 - 9a  + 0.25a²

When I get a chance I'll type them all up. It does make you wonder why the vast majority of textbooks and worksheets on factorising these days simply have questions like this:

Factorise x² +7x

Factorise x² + 5x + 6

Factorise x² - 9

and maybe this kind of thing for stretch:

Factorise 3x² + 10x + 8

Factorise 2x² - 18

Is that really the best we can do? We could at least change the order of the terms! No wonder so many of our students lack algebraic fluency when they get to A level.

If you're thinking that this factorising exercise from the 1950s is a bit tricky, you will be relieved to hear that in the same book there are a number of exercises breaking down the factorising skills into stages, leading up to the 'Miscellaneous Factors' activity which brings it all together. For example there is a whole section on 'Factors by Grouping' which explains how to factorise expressions like ax + 2x + 3a + 6. I'm not sure this skill is widely taught these days.

I have plenty of students who would love to get stuck into these questions. Back in 2015 I wrote the post 'Stretching Practice' which is about where to find good practice resources for high attainers. There's a decent selection of resources available, but nothing quite at the same level as the exercises from 1950s textbooks. I think that the closest online resources for developing algebraic fluency are some of Don Steward's tasks, like this excellent difference of two squares exercise:

I wish I could show you every exercise from 'A Classbook of Algebra'. There are so many great questions. I'll just share a few more examples...

Under the title 'Easy Brackets' we find questions that many teachers would now use as extension work in a lesson on expanding single brackets:

And under 'Miscellaneous Easy Brackets' the questions look very different to what we now consider to be 'easy':

 

When we teach 'collecting like terms' I doubt many of us use exercises like this one on 'Addition and Subtraction of Polynomials':

Check out the last question: 'To the excess of 6 - x + x² over 5 + x² - 3x add x² -3x + 4'!

Do you want to check that your students really know how to expand brackets and solve equations? Try some of these:

Here we have double brackets too:

I wrote about multiplying negatives in this post, but the resources I featured didn't include algebra like this exercise does:

Finally (though I could go on all day!), here's something for your indices lesson:

If only I had time to type all these up!

I hope you enjoyed looking at exercises from the 1950s as much as I did.

Mock Season

Many schools have Year 11 mock GCSE exams over the next few weeks. In case you have time to run a few revision lessons before your mocks start, this post provides a quick reminder of some great resources.

Access Maths
Access Maths is an excellent source of revision activities for the classroom. There's a large selection of resources on the 9 - 1 Revision Material page for both Foundation and Higher tier.

Corbett Maths
Even if you don't use Corbett Maths 5-a-Day on a daily basis then you still might find them useful in revision lessons. In my post about Structured Revision Lessons, I wrote about how I used 5-a-Day in the run up to last year's GCSEs. At five different difficulty levels, they're suitable for all GCSE students.

MathsBot
On Mathsbot.com you can generate GCSE revision grids containing questions for Foundation, Crossover or Higher. These grids can be displayed on the board or printed onto worksheets for revision lessons.

There are a number of other GCSE resources on MathsBot that might be helpful for mock revision.

PinPoint
Many schools use a QLA (question level analysis) to analyse performance by topic after exams. If you register with PinPoint Learning you can get QLA spreadsheets for free, all ready to complete, for every practice paper and past paper for all awarding bodies. So schools don't need to create their own QLA spreadsheets.

PinPoint Learning also offers a tool where you can upload your completed QLAs (or have students input their own marks) and produce a tailored booklet of questions for every student. A departmental analysis of mock results can also be generated. This normally comes with a subscription costing £400 a year but they are currently offering a free trial until 25th January.

More Resources
There are loads more revision resources in my post GCSE 9 - 1 Revision Resources and my post about Revision Clocks.

It's also worth reading my post Higher GCSE revision from 2015. I wrote it for the old GCSE but all the resources featured are still useful, including the excellent activities on Don Steward's practice blog.

Good luck with the mock marking everyone!

5 Maths Gems #80

Welcome to my 80^th gems post. This is where I share some of the latest news, ideas and resources for maths teachers.

1. Times Tables Tool
La Salle Education have made a free version of their Times Tables app available to everyone. It includes multiple representation of multiplication and division facts. I look forward to using this with my daughter when she starts learning about multiplication.

2. Twinkl Taster Pack
I blogged about Twinkl's new secondary maths resources back in Gems 65. They've now shared a free taster pack which includes a set of revision mats suitable for Foundation GCSE students.

3. Quadratics Resources
Thanks to @TeacherBowTie for sharing some lovely quadratics resources including an A3 quadratics consolidation activity which would work well for revision and a problem solving activity for practising factorising.

I've added both resources to my algebra resource library.

4. Times Table Facts
This times tables resource from Anthony Clohesy is well worth a look - it shows the only 28 times table facts students need to learn, arranged in order from important (at the bottom) to difficult (at the top). While you're there, check out the rest of his website thechalkface.net.

5. Universcale
Thanks to my lovely colleague Jane Zimmermann for telling me about Nikon's 'Universcale' tool. This is great for exploring magnitude and measure. It reminds me of the popular 'The Scale of the Universe' that I shared in Gems 12, way back in 2014.

Update
In case you missed it, my post 'The Top 5 Christmas Gifts for Maths Teachers This Year' was published by TeachWire. While you're thinking about your wish list, have a look at Craig Barton's new book 'How I Wish I'd Taught Maths' which is now available to pre-order. I've been very lucky to have a sneak preview of this book - it's fantastic. Look out for my blog post about it soon.

Did you catch my post about MathsJam? If you're a maths enthusiast then do try and get involved in your local MathsJam or come along to the annual gathering next year.

In September I took part in a researchED debate called 'When the maths hits the fan: what do the GCSE results really mean?'. The recording of that session has now been published online - if you have a spare 40 minutes, do have a listen.

If you intend to come to BCME (the hugely exciting maths conference taking place at Easter that I wrote about here) please remember that you only have a couple of weeks left to apply for a bursary. I've applied!

You also only have a couple of weeks left to share your view about the proposed subject association amalgamation - please add comments here.

Mock GCSE season is now upon us - look out for my upcoming blog post about the best revision resources and tools to support students in their exam preparation.

I'll leave you with this great question from Mark Chubb‏ (@MarkChubb3). Do these two have the same area? Same perimeter? Will this always be true no matter how they are put together?