When you teach functions your students get to revisit some key algebraic skills including solving linear and quadratic equations, simplifying and rearranging formulae, and substitution. Given that the new higher GCSE is 30% algebra, revisiting these core skills is definitely worthwhile at this point in the course.
In the legacy GCSE the only use of function notation was in graph transformations. It always felt a bit wrong to talk about f(2x), f(x + 3) etc when the notation f(x) was previously unknown and wasn't used elsewhere. The GCSE course flows much better now we are able to cover functions followed by graph transformations (which has now been reduced to only translations and reflections).
For Higher GCSE 9 - 1 we have three main areas to teach in this topic:
- Inputs and outputs
- Composite functions
- Inverse functions
This is similar to the current functions content at A level, though A level also includes domain and range. This functions content will remain in A level maths under the new linear specifications. Meeting this topic at GCSE will certainly benefit students who go on to take A level maths.
This post aims to support GCSE teachers who are teaching this topic for the first time.
Specification
At both Foundation and Higher tier, students are required to "interpret simple expressions as functions with inputs and outputs". At Foundation the main focus is on function machines. At Higher, there's more: "interpret the reverse process as the ‘inverse function’; interpret the succession of two functions as a ‘composite function’". In AQA's Teaching Guidance, we are told that Higher tier students should be able to:
- understand that a function is a relationship between two sets of values
- understand and use function notation, for example f(x)
- substitute values into a function, knowing that, for example f(2) is the value of the function when x = 2
- solve equations that use function notation
- understand, interpret and use composite function fg(x)
- understand, interpret and use inverse function f-1(x)
OCR's specification differs slightly, saying 'knowledge of function notation will not be required'.
Challenges
When teaching inverse functions I first showed my students how to work backwards through a function machine. I then showed them the procedural 'changing the subject method' that I teach at A level (similar to the method explained by Edexcel below).
My students have mock GCSE results ranging from Grade 4 to Grade 8. Although they had no problem finding the inverse of simple functions, some struggled to find the inverse of this function:
They were taught how to change the subject when the subject appears twice (ie when you have to factorise) in Year 10, but many couldn't remember it. This was a good opportunity to teach it again.
I set them a fairly challenging homework with questions extracted from Edexcel's excellent new content resources. Many struggled with the second part of this question:
The function f is such that f(x) = 2x - 3
Find (i) ff(2) (ii) Solve the equation ff(a) = a
Composite functions are definitely the most challenging part of this topic. When I taught my composite functions lesson I was convinced that they'd all understood the 'right to left' order, but when I gave them their weekly quiz the two composite functions questions were answered incorrectly by a number of students. They got the order wrong.
Most of my class also got this question wrong:
I included this partly to test their recollection of negative and fractional indices but it actually showed a misconception relating to the order of operations. Even some of my strongest students incorrectly selected answer B because they'd done the multiplication before the index.
Questions for my weekly quizzes (which I wrote about here) are always taken from diagnosticquestions.com.
Exam Questions
Mel's collection of exam questions by topic from the sample and specimen papers continues to be very useful. There are some lovely exam questions on functions - here's an example:
 |
| Source: AQA, via JustMaths |
These exam questions collated by mathsgenie.co.uk are also helpful (solutions here).
I used four sources of questions in my functions lessons:
- the brilliant new content resources from Edexcel (download the full set here under 'resources')
- extracts from A level Solomon worksheets
- composite and inverse functions activities from MathsPad.co.uk (subscription required)
- examples and exercises from this CIMT textbook chapter
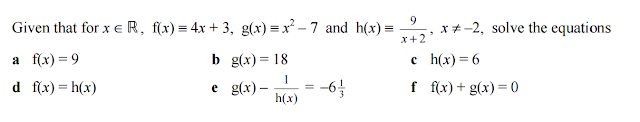 |
| Extract from C3 Functions Solomon Worksheet A |
AQA has a good Bridging Unit Resource Pocket on functions. OCR has a Language of Functions topic check-in which is really good for function machines.
Writing Algebra is a nice function machine activity from Stacy Brookes.
See my algebra resource library for more resources.
If you're looking for illustrations to use in your lesson then this website is helpful. I like what they've done here for composite functions:
It's worth mentioning that the function notation we use at school may differ to that used by universities - read this thread for more on this.
I hope that you found this post useful and that you enjoy teaching functions as much as I did!


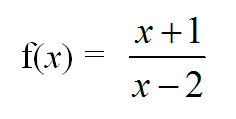





Thanks to David Butler (@DavidKButlerUoA) for his post which describes a much more mathematically sound way to find an inverse function than the procedure described above. http://blogs.adelaide.edu.au/maths-learning/2017/01/19/finding-an-inverse-function/
ReplyDeleteHi, sorry about the mix up with the my last post. I am new to blogging and did it subconsciously. I did not mean to use your words/ideas. Taken the post down with immediate effect. Thanks
ReplyDeleteNo harm done. Thanks for getting in touch. I'm always happy for ideas to be shared with a wider audience, but it's best done in your own words. Please don't worry.
DeleteThank you for understanding - would really appreciate it if the picture is taken off twitter? Apologies again
ReplyDeleteDone!
DeletePlease could you inform me on the answer to ' f(x) = 4x^-1/2 what is f(4).
ReplyDeleteFirst do the index: 4^(-1/2) = 1/2
DeleteThen do the multiplication: 4 x 1/2 = 2
So the answer is 2.