Last week I blogged about our Year 8 assessments. I set out the principles we follow when we write our Key Stage 3 assessments, and I shared examples of the questions that challenged our highest attaining students.
Today's post is about Year 9. My school's Year 9 cohort has a very wide range of maths attainment, which was further exacerbated by the lockdowns in Year 7 and 8. One notable feature of this year group is how incredibly good the high attaining students are. The top set teacher finds it hard work to sufficiently challenge them in lessons. So when I made the end of year assessment, I had to ensure there were plenty of questions in there to make them think. I don't want anyone coming out of a maths assessment bragging that they found it really easy.
Here are some of the more challenging questions from our end of Year 9 assessment.
Ratio
At a concert the ratio of men to women is 5 : 3.
The ratio of women to children is 7 : 4.
Show that more than half of the people at the concert are men.
This was a middle-of-the-paper question. It's not massively challenging - I taught set four out of five and a few of them managed to get full marks on it. But I wanted to include it here because it's a nice question requiring a bit of reasoning. It was originally from an AQA specimen GCSE paper.
A more difficult ratio question was this one from Edexcel, which also tested another Year 9 topic: changing the subject.
The ratio (y + x) : (y - x) is equivalent to k : 1.
Find a formula for y in terms of k and x.
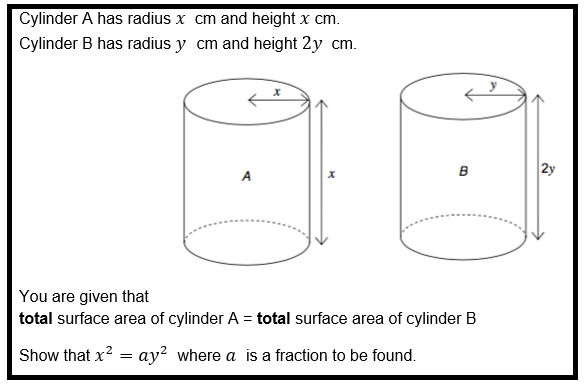
Surface AreaSurface area is a great topic because it presents many opportunities for problem solving and reasoning. For example, this classic question may have been fairly straightforward for a high attainer, but I like the way it's also accessible to anyone who does a bit of thinking. I was delighted that a few students in my class worked this out. We put it in our non-calculator paper so it also tested their arithmetic.
The total surface area of a cube is 294cm2.
Work out the volume of the cube.
A slightly more difficult question was this one from Edexcel. It doesn't have any particularly challenging reasoning in it, but has got a multiple steps to work through, including unit conversion which might be missed. I like questions where students have to identify that they need to work with surface area rather than volume.
The most challenging surface area question I included was this one from AQA. Very few students could do this, even our highest attainers. We will revisit questions like this in Year 10.
Bounds
I like this coal question from WJEC. In Year 9 we teach bounds and error intervals for the first time. We introduce some basic bounds calculations, but go into greater depth on this at GCSE. This question fitted perfectly. However, I thought our students would find it easier than they did. I had it near the start of the paper, but most the students in my class only picked up one mark on it. My students are all working at a Grade 4 level though. Our higher attaining students had no problem with this one.
Probability
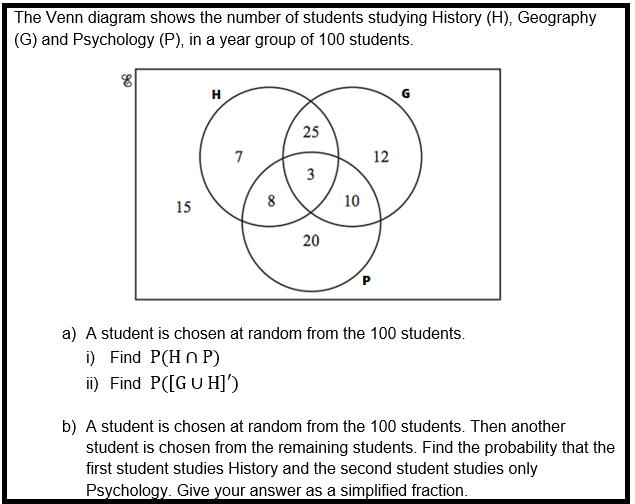
We taught Venn Diagrams to Year 9 this year. There were some fairly straightforward Venn diagram questions nearer the start of our end of year assessment, where students basically just had to complete various Venn Diagrams. But for challenge I wanted to test understanding of notation as well as probability, so I adapted an OCR AS level question. Only our very best mathematicians answered this correctly.
Algebraic Proportion
Algebraic proportion can be incredibly procedural. As long as students read the question carefully, once they know how to do it, it's almost a guaranteed five marks. So I included a non-calculator proportion question that was a bit different to questions they'd seen before. What I liked about this was the accessibility: no one from my class got all the marks, but they did manage to pick up one or two.
Right-Angled TrigonometryThis question was my pièce de résistance. I figured that if our super clever Year 9s breezed through all the other challenging questions I threw at them, they would surely have to stop and think at this point. This SQA question is designed to be solved using the Sine Rule. But our students don't do the Sine Rule until Year 10. This question can be done with right-angled trigonometry. The way I did it was by splitting the base into x and 350 - x, then forming two equations for the height and equating them. Even if our students managed to get this far, solving the equation would be fairly challenging for them because they haven't seen anything like this before.
As it happened, none of our Year 9s managed to solve it in the way I envisaged. But one very smart student came up with a genius (albeit inefficient!) method of trial and improvement. I yelped with joy when I realised what he'd done:
It's such a delight to see students using creative approaches like this.
I also found some great challenging questions involving standard form and percentages, but I will stop at this point otherwise this blog post will go on forever! Like I said in my last post, there are numerous places we can find good assessment questions for Key Stage 3. It's a shame they aren't centrally produced anymore - the old KS3 SATs contained great questions, but at least we can still draw on those to make our own assessments.
If you have any good Year 9 assessment questions you'd like to share, please tweet me.
Thanks for reading!






No comments:
Post a Comment