- no book existed about the common misconceptions in each topic.
- no book existed about the various methods that can be taught in each topic.
I felt that both of these should be standard reference books for trainee maths teachers. But they didn't exist. I addressed the latter (see my book 'A Compendium of Mathematical Methods') but no one has fully addressed the former. We still don't have an easy-reference book or website featuring all the common misconceptions in one place. Instead, we repeat the mantra 'inexperienced teachers should learn about common misconceptions from their experienced colleagues'. That's a great idea, unless you find yourself working in dysfunctional maths department where no one talks maths. Then you just have to work it all out for yourself.
I think back to the time I tweeted a misconception that took me by surprise when I was marking a Year 7 fractions quiz.
Just because we haven't personally seen a misconception, it doesn't mean it doesn't exist. Sometimes we just haven't asked the right questions.
A flaw in my explanation
Occasionally I see a student doing something in a lesson and realise it has resulted directly from my own flawed explanation. So I reflect on this, and I adjust my explanation the next time I teach it. I experienced this recently when I gave my Year 8 students a test on expanding double brackets. One student did well on every question, until he got to this one:
Expand and simplify (𝑥-2 + 4𝑥10)(𝑥2 + 5𝑥3)
I was delighted that this student knew that 𝑥2 ✕ 𝑥-2 = 1, demonstrating his knowledge of index laws (other students wrote 𝑥0 which was also acceptable).
However, a misconception relating to expanding arose that I wouldn't have spotted if I hadn't used this particular question.
Can you see what he's done? He seems to have assumed that the two diagonal cells can always be simplified. So there's a misconception in his underlying algebraic knowledge that needs to be addressed (i.e. that 4𝑥12 + 5𝑥 can be simplified). There's also a step in the expansion procedure that he has fundamentally misunderstood. A couple of other students did something similar.
I take the blame for this one, even though I don't teach the popular 'sausage method' which could directly lead to this misconception. In case you don't know what the 'sausage method' is, check out the video here to here to see it in action (there are dozens more videos like this). Basically it involves drawing a ring around the two diagonal terms that can be simplified (the ring is sometimes referred to as a sausage, balloon or peanut).
Of course, the circled terms can only be simplified in certain expansions, so we should be careful to avoid implying that this ring can always be drawn.
So what did I do wrong in my teaching? Well in my initial modelling I always completed the grid then wrote out the four terms underneath the grid before simplifying them. I did that every time, until my students had built up some fluency in using the grids. Then I got a bit lazy and rushed my modelling, to the point where sometimes I skipped writing out the four terms underneath the grid, and took to drawing a ring around the like terms. I distinctly remember doing this when demonstrating a triple bracket expansion. So although I never said that 'drawing a sausage' is part of the procedure, and I certainly never said 'these two terms can always be simplified', I may have accidentally implied this in my modelling. Lesson learnt! Not every misconception is a direct result of a flaw in my explanation, but I think this one probably was.
Misconception baggage
Pre-empting misconceptions
As I mentioned earlier, our students come to us with ingrained misconceptions that need addressing - sometimes the student has been carrying that misconception around for years. On a daily basis I'm furious at whoever was responsible for inventing the acronym BIDMAS because it leads directly to a totally avoidable misconception. I'm not opposed to mnemonics at all, but they should have chosen a better one. Even BIDMSA would have preferable. Anyway, I'm not here to rant about BIDMAS (I have a video about it here) but this is something that we know is a big problem. I shouldn't have been surprised when I saw the classic mistake recently, but what surprised me was the context:
I have a class of very strong mathematicians in Year 10, and one of the best students in the class asked me for help on this question:
'Write as a surd in simplest form: 10sin60 - 12tan30 + 8cos30'.
This was in a task on simplifying expressions involving exact trigonometric ratios, which is basically an exercise in manipulating surds.
"Miss, can I just check something with this question. I have to add 12tan30 and 8cos30 first, right? Because of BIDMAS?"
Who knew that the order of operations would be a problem in my lesson on exact trig values...
There's some debate about whether we should show our students common misconceptions up front. Some people think it might confuse them, but I'm all for it. In my teaching I directly show the mistakes people make and we discuss the reasons, and I make it clear what's gone wrong. That's not to say it always works though.
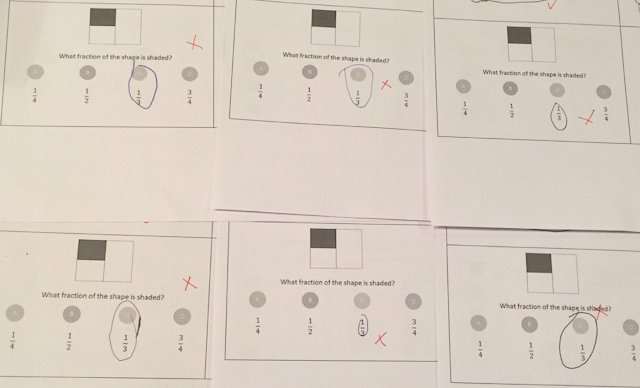
When teaching angles on a straight line, I'm careful about the wording (I always very specifically say 'adjacent angles on a straight line sum to 180') and I talk up front about how the angles need to be next to each other - they need to form a half-turn - in order to add up to 180. As a class we explore and acknowledge the common misconception. Yet still I have one or two students who do things like this:
Even though I don't have 100% success rate at eliminating all misconceptions, I still think addressing them head-on is worthwhile.
We can also address misconceptions through task design and curriculum sequencing. I recently had a Year 8 student who was factorising this expression:
4abc2 + 10a3b2c
He put up his hand to ask me whether the index in the first term only related to the c. A good question! It then occurred to me that I hadn't explicitly addressed this in my teaching, but I had previously designed a resource exactly for this purpose. I have an exercise on substitution that aims to draw out misconceptions around algebraic notation - see extract below.
I used this in a subsequent lesson with the same class. When circulating during the lesson, I spotted that a number of students had incorrectly evaluated Questions 10 to 15 by multiplying first. I know this is a common misconception so I should have probably done some more work on mini-whiteboards at the start of the lesson to draw it out and address it.
A misconceptions journal
I made a note of a few misconceptions this term because I thought they might be interesting to blog about. So I ended up with a notepad on my classroom desk where I jotted down some things students said in lessons. This made me reflect on whether I should make a habit of doing that - keeping a log or journal of misconceptions that I could later reflect on and discuss with colleagues. Perhaps all teachers should do this. It's probably totally impractical though - over the course of a day's teaching we process dozens of misconceptions. And this isn't a bad thing - good teaching should be designed to draw them out and address them! If we're not seeing misconceptions, it doesn't mean they don't exist. They may just be hiding.
I made a note of a few misconceptions this term because I thought they might be interesting to blog about. So I ended up with a notepad on my classroom desk where I jotted down some things students said in lessons. This made me reflect on whether I should make a habit of doing that - keeping a log or journal of misconceptions that I could later reflect on and discuss with colleagues. Perhaps all teachers should do this. It's probably totally impractical though - over the course of a day's teaching we process dozens of misconceptions. And this isn't a bad thing - good teaching should be designed to draw them out and address them! If we're not seeing misconceptions, it doesn't mean they don't exist. They may just be hiding.
Finally, I will end on a positive, with a lovely quote from the late Malcolm Swan:
"Frequently, a ‘misconception’ is not wrong thinking but is a concept in embryo or a local generalisation that the pupil has made. It may in fact be a natural stage of development."
 |
| Misconceptions posters from classicmistake.nhost.uk |
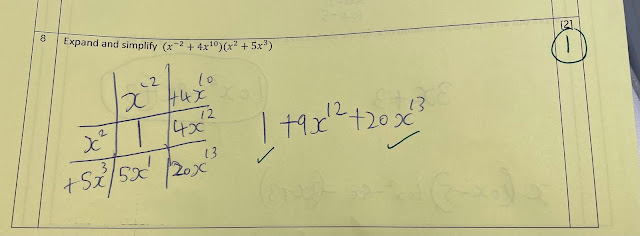



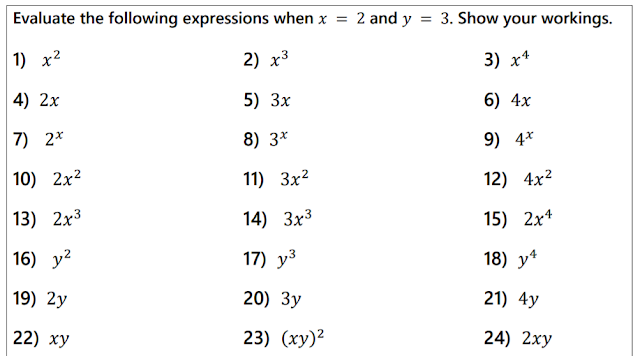

Hi Jo
ReplyDeleteDon't know if you ever saw the document from Counton with 22 common misconceptions?
Colleen Young has a copy on her website https://colleenyoung.org/wp-content/uploads/2021/08/misconceptions122.pdf
Thanks! That's helpful. I have that one listed on my misconceptions page: https://www.resourceaholic.com/p/misconceptions.html but the link is now broken! I wish these old websites would stop disappearing. It's a fab document. Not sure if the definitive easy-reference guide to all misconceptions that I'm looking for, but it is very good.
DeleteHi Jo, I think I have found the document on Colleen Young's website - https://colleenyoung.org/tag/misconceptions/
DeleteCounton was a great project but when funding ran out the website fell by the wayside - such a waste of everyone's efforts!
I hope to meet you at the Joint Maths Conference in Warwick in April
Caroline Ainslie
Hi Jo
ReplyDeleteGreat blog! Thank you for sharing and for your honest reflections.
A book I used a few years ago was 'Children's Mathematics 4-15. Learning from errors and misconceptions' by Julie Ryan and Julian Williams. Your blog has inspired me to revisit it with the knowledge and experience I now have.
Thanks
Thank you. Sounds like an excellent book - I'll check it out.
DeleteThis is true.
ReplyDeleteHi there, have you seen:
ReplyDeleteChildren's Understanding of Mathematics: 11 to 16 by CSMA Mathematics Team, et al, K.M. Hart (Paperback, 1989)
Excellent book on misconceptions.
Thank you! I will check it out
DeleteHello Jo, I did a PD at Melbourne University a few years back and it was on Purposeful teaching. This PD examined misconceptions and a diagnostic tool called SMART tests. This resource is now offered through Pearson known as Pearson Diagnostic. https://www.pearson.com/en-au/educator/diagnostic/ I also found this link to a site on decimals we were provided with at the time. https://extranet.education.unimelb.edu.au/SME/TNMY/Decimals/Decimals/index.htm Malcolm
ReplyDeleteThanks Malcolm! I will have a look at this.
DeleteDan Meyer posted something relevant about this recently when he was acting as a substitute teacher...
ReplyDeletehttps://danmeyer.substack.com/p/my-substitute-teaching-was-saved?r=ivzyu&utm_campaign=post&utm_medium=email