This is a contribution to the series of writings called 'Dose of Don', begun by Anne Watson, which delve into the collection of tasks on Don Steward’s blog. This piece is written by Sam Blatherwick (@blatherwick_sam). Many thanks to Sam for giving me permission to share his writing here. For the background on this series, please see the post Lines and Angles on Square Grids.
Don was very generous with his tasks and it is hoped that you will return this generosity in the way he requested before he died, namely to donate to justgiving.com/fundraising/jessesteward.
Don Steward’s median blog was, and remains, a great resource for tasks and there are certain sets of questions that resonate when you come to teaching a topic. You’ll have your own soft spots, but exercises that come to mind for me are the recurring decimals calculations task and the small data set averages problems. Above all though one that stands out when I come to teaching ratio is the ‘Asterix and Cleopatra’ problem sheet. When I first saw it, it felt so modern, simply because we were suddenly encountering questions like this all over the GCSE papers but it didn’t feel like there were any questions in textbooks that were replicating them.
My initial reaction to teaching this was, how? I had my own elaborate algebraic procedures, but I had been chastised in the past by the students for reaching for algebra whenever the going got tough, it wasn’t something that was coming to naturally to students. And then, when you work this out by hammering it with algebra, you were kind of disappointed – like there must be a faster way.
My initial reaction to breaking this down then was to list equivalent ratios, and this is still something I recommend to students when they don’t know what to do. If you do this the answer drops out pretty fast:
What if they had 3:5 – you’d get 1 and 7 – this doesn’t work.
What if they had 6:10 – you’d get 4 and 12 – this does work.
Don crushes the idea that this will be a cinch with the next one:
Initially: 5:6 = 40:48
Now: 7:8 = 42:48
So we can now see those two marbles in action – Jan had 40 marbles and Kim has 42.
Later we come to a problem again – and if we’d looked back at Anthony and Cleopatra we’d have noted that a method of things being fixed wouldn’t really have worked for us.
Later we come to a problem again – and if we’d looked back at Anthony and Cleopatra we’d have noted that a method of things being fixed wouldn’t really have worked for us.
What’s fixed here? Not the red socks, and not the white socks. For a while here I was under the impression we were in a pickle when it came to questions like this and just had to go back to listing. Alas, if we go back to listing here, we have to go a very long way.
Until I was introduced to what was actually fixed – and in this case our fixed part was our number of socks – the total of the ratio.
So each part of the original ratio is 3 pairs of socks, so we have 135 white pairs of socks and 75 pairs of red socks.
And this is where I thought the story ended, with a lovely straightforward universal method for these problems – decide what you want to be fixed and fix everything in line with it. Then I was in a training session and someone stuck up these questions and asked us to have a go at them, before sharing the algebraic methods that his students did.
And I scoffed and went “oh ho ho, how enlightened I am knowing a better way..!”
There was a discussion around the Sine Rule on Twitter recently where the opinion was aired that as maths teachers we have a tendency to “algebratise” everything too quickly. I’m not sure I saw it at the start of my career, but I think I tend to agree now. Isn’t there something to be said that maths teachers do “algebratise” though? And how do we develop that as a skill?
What about that ‘better way’ I was so smug about? It leads us to the answer, but is it just an endpoint? Where does this lead to? In fact I considered, what if in fact these questions are a lovely vehicle for also introducing some algebraic work? Even after the ‘universal’ method has been introduced there’s running to be had on playing around with algebra in these questions and playing around with how we introduce unknowns.
So going back to the original question:
Until I was introduced to what was actually fixed – and in this case our fixed part was our number of socks – the total of the ratio.
So initially we have: 9:5:14
And subsequently we have 3:2:5
Before: 9:5:14 = 45:25:70
After: 3:2:5 = 42:28:70
And this is where I thought the story ended, with a lovely straightforward universal method for these problems – decide what you want to be fixed and fix everything in line with it. Then I was in a training session and someone stuck up these questions and asked us to have a go at them, before sharing the algebraic methods that his students did.
And I scoffed and went “oh ho ho, how enlightened I am knowing a better way..!”
There was a discussion around the Sine Rule on Twitter recently where the opinion was aired that as maths teachers we have a tendency to “algebratise” everything too quickly. I’m not sure I saw it at the start of my career, but I think I tend to agree now. Isn’t there something to be said that maths teachers do “algebratise” though? And how do we develop that as a skill?
What about that ‘better way’ I was so smug about? It leads us to the answer, but is it just an endpoint? Where does this lead to? In fact I considered, what if in fact these questions are a lovely vehicle for also introducing some algebraic work? Even after the ‘universal’ method has been introduced there’s running to be had on playing around with algebra in these questions and playing around with how we introduce unknowns.
So going back to the original question:
There are so many ways we can introduce an unknown here. What if we said the number of shares that Asterix has is x?
Originally:
Originally:
Afterwards:
So:
What about if Cleopatra has x?
What about if the total was x?
A potential stepping stone from ratio to algebra depends on the models you use for ratio. I tend to build from a “boxes” method of ratio to demonstrate 3:5 as
What about if the total was x?
A potential stepping stone from ratio to algebra depends on the models you use for ratio. I tend to build from a “boxes” method of ratio to demonstrate 3:5 as
Where the open box is a vessel that has to contain the same as all the other boxes.
If we use that open box as x then we are solving a question where x is one part of the original ratio, and we can apply that to the Asterix and Cleopatra problem.
Originally:
Then:
So:
It’s interesting to note that Don himself notes in his introduction to the tasks that the algebraic way is “relatively unthinking”!
In conclusion, not everything needs to be ‘algebratised’ and often other numerical ways of solving problems can give you solutions to problems in elegant ways. However, the answer need not be the end and exploring different algebraic ways of exploring these problems can help your students fluency and competency with algebra.
In conclusion, not everything needs to be ‘algebratised’ and often other numerical ways of solving problems can give you solutions to problems in elegant ways. However, the answer need not be the end and exploring different algebraic ways of exploring these problems can help your students fluency and competency with algebra.




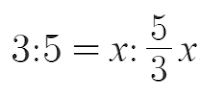
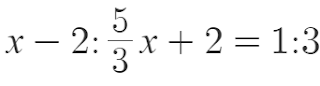



Some really great ways to deal with ratios both with and without algebra!
ReplyDeleteCleo got two and her share increased from 5/8 to 3/4.
ReplyDeleteSo 2 = 1/8.