Background
Imagine designing a mathematics GCSE from scratch. What topics would you include? There's a lot of mathematics to choose from. You only have to glance at an old textbook or O level paper to see that the topics studied at secondary school have changed considerably over the last century. Have circle theorems always featured on the UK curriculum?
Looking back at the 1957 O level Syllabus, we have the following:
 |
| Extract from 1957 O level maths syllabus |
In the 1957 O level exam there were many questions relating to circle theorems, including a number of proofs. The question below is perhaps the easiest, and is similar in style to the questions seen on current GCSE papers. Our students might enjoy having a go at questions like this - the maths that their grandparents did at school.
 |
| 1957 O level question |
Interestingly the wording (but not the substance) of the circle theorems content on the 1974 O level Syllabus differs notably from the 1957 Syllabus. Again, circle theorems feature heavily in the Geometry section of the 1974 O level exam. In the question below, our current GCSE students would be able to do part a, but not part b.
 |
| 1974 O level question |
 |
| 1984 O level question |
 |
| Extract from Edexcel GCSE 2012 Mathematics A specification |
Thankfully the new AQA specification is less vague, confirming the continuation of the existing content.
The new OCR specification contains a similar level of detail.
So it's long been accepted that circle theorems are worth including in secondary mathematics education. Although there's been a small reduction in the range of theorems covered over the last 60 years, the majority have survived. Circle theorems may have little direct application in 'real life', but that doesn't matter. Mathematicians enjoy applying circle theorems to solve interesting geometrical problems. The trickier problems can really test our logical thinking skills and are particularly satisfying. I'm pleased that circle theorems are here to stay. So let's look at a few teaching ideas.
A good place to start when teaching circle theorems is a recap of angle facts relating to triangles and parallel lines. Most teachers then get their students doing some exploration into angles in circles. Once each theorem is established, students should do a lot of practice, starting with simple cases then moving onto more complex questions involving more than one theorem. We need to look at proofs along the way too.
Vocabulary
There's a lot of new vocabulary in this topic. First we have the parts of a circle - your students could explore these using this Geogebra tool from mr-mathematics.com. Once they're familiar with the vocabulary, they could label the key parts of a circle on paper plates as in this blog post from Mr Collins.
This is also a good opportunity to talk about etymology - tangent originates from the Latin tangere 'to touch' and arc originally referred to the sun's apparent motion in the sky. Segment (think oranges) and sector (think pie charts) are both from the Latin secare 'to cut'. Diameter is from the Greek dia- "across, through" and metron "a measure".
As well as the parts of a circle, we also have new words in the descriptions of the theorems. For example James Tanton gives us this:
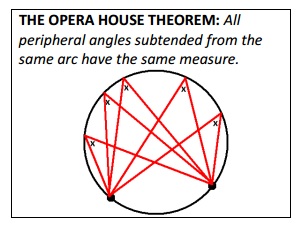
In class you may refer to theorems using catchy names such as opera house (or bow-tie or crown), arrowhead, ice-cream (or hat), but in a GCSE exam your students will need to use more formal language. Although the words peripheral and subtend are not essential, instead of avoiding them why don't you encourage students to deduce the meanings? Subtend is from Latin 'to stretch underneath'. I don't use the word peripheral in this topic, but it can be linked to peripheral vision which students may be familiar with.
In my post about vocabulary I make some suggestions for activities to support students when you introduce new key words, such as vocabulary knowledge surveys and literacy walls.
Investigations
It's nice to give students the opportunity to investigate the angles in a circle using ICT, geoboards (virtual or real), worksheet investigations or paper folding. I love this series of Geogebra worksheets from The Maths Teacher. Students can play around with the angles on screen then answer the questions provided. In Folding Circles: Exploring Circle Theorems through Paper Folding from the NCTM, students manipulate paper circles to explore circle theorems (scroll down to theorems three and four in the instructions). I also like these two simple paper-based demonstrations: angle at the centre and angles in the same segment.
 |
| Source: Wikipedia |
A good place to start when teaching circle theorems is a recap of angle facts relating to triangles and parallel lines. Most teachers then get their students doing some exploration into angles in circles. Once each theorem is established, students should do a lot of practice, starting with simple cases then moving onto more complex questions involving more than one theorem. We need to look at proofs along the way too.
Vocabulary
| Paper plate vocab from Mr Collins |
This is also a good opportunity to talk about etymology - tangent originates from the Latin tangere 'to touch' and arc originally referred to the sun's apparent motion in the sky. Segment (think oranges) and sector (think pie charts) are both from the Latin secare 'to cut'. Diameter is from the Greek dia- "across, through" and metron "a measure".
As well as the parts of a circle, we also have new words in the descriptions of the theorems. For example James Tanton gives us this:
In class you may refer to theorems using catchy names such as opera house (or bow-tie or crown), arrowhead, ice-cream (or hat), but in a GCSE exam your students will need to use more formal language. Although the words peripheral and subtend are not essential, instead of avoiding them why don't you encourage students to deduce the meanings? Subtend is from Latin 'to stretch underneath'. I don't use the word peripheral in this topic, but it can be linked to peripheral vision which students may be familiar with.
In my post about vocabulary I make some suggestions for activities to support students when you introduce new key words, such as vocabulary knowledge surveys and literacy walls.
 |
| 'Name the line' vocabulary exercise |
It's nice to give students the opportunity to investigate the angles in a circle using ICT, geoboards (virtual or real), worksheet investigations or paper folding. I love this series of Geogebra worksheets from The Maths Teacher. Students can play around with the angles on screen then answer the questions provided. In Folding Circles: Exploring Circle Theorems through Paper Folding from the NCTM, students manipulate paper circles to explore circle theorems (scroll down to theorems three and four in the instructions). I also like these two simple paper-based demonstrations: angle at the centre and angles in the same segment.
 |
| Extract from Folding Circles (NCTM) |
Another idea for investigating angles in circles involves hula hoops - this originates from the guest post Circle Theorems and Hula Hoops on Mr Reddy's blog back in 2012. Read the post to see how the lesson works and download the resources. It's also worth reading this post by Kelly Achtymichuk (source of the pictures below) and Mr Collins' post 'Circle Theorems & Hula Hoops!!' to see how other teachers have adapted the idea.
Cyclic Quadrilaterals
Cyclic Quadrilaterals
All triangles have a circumcircle but not all quadrilaterals do. Ask your students to sketch an example of a quadrilateral with circumcircle (eg a square) and one without (eg a rhombus).
I like the question below (from this CIMT exercise) to develop understanding of the word concyclic.
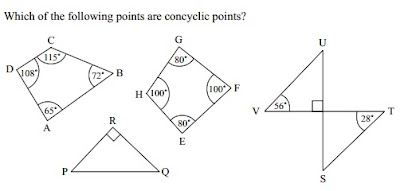 |
| Question from CIMT |
Proof
 Students should have a go at working the proofs out themselves. But they're not accustomed to proof, so they'll probably need some direction. For example, when they're proving that the angle in a semicircle is a right-angle, you could show them the step pictured and ask 'how would you get to this step?' And where would you go from here?'.
Students should have a go at working the proofs out themselves. But they're not accustomed to proof, so they'll probably need some direction. For example, when they're proving that the angle in a semicircle is a right-angle, you could show them the step pictured and ask 'how would you get to this step?' And where would you go from here?'.I also really like this activity from rhemsley on TES which makes the proofs more accessible by starting with numbers before generalising.
The NCETM also gives us this proof worksheet where students fill in the missing words.
Tangent proofs are not currently on the GCSE syllabus but if you want to prove the tangent theorems with your class, watch James Tanton's video Tangent Theorems for Circles and the Pythagorean Theorem beforehand - the explanations are very clear.
If you want circle theorems and proofs on your classroom wall then these posters from danbar1000 on TES are great.
Resources
If you're planning a sequence of lessons on circle theorems then you'll find plenty of useful worksheets and activities listed in my shape resources library.
If you're planning a sequence of lessons on circle theorems then you'll find plenty of useful worksheets and activities listed in my shape resources library.
In my last gems post I mentioned the free app Angles? - Let's solve figures problems! by Gakko Net Inc. If your students have access to iPads in lessons then this is a brilliant app for practice. It starts off with triangles and parallel lines but you can skip ahead to circle theorems.
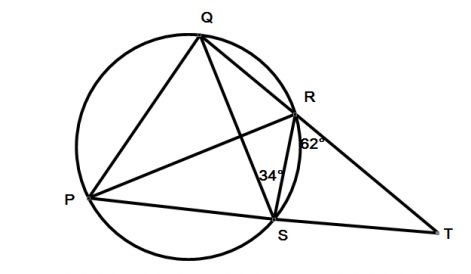
Particularly complex circle theorem questions, or 'busy' diagrams (like the question below), could be enlarged on A3 paper - this would be a good opportunity to use the acrylic sheets suggested in Jeremy Denton's post 'Improving students' collaboration using acrylic sheets'.
Memorising the theorems
Enough practice of using circle theorems might be sufficient to memorise them, but in this post Don Steward suggests that there might be benefit in chanting the theorems. I've not tried this yet but back in primary school I learnt my times tables by chanting - it seemed to work well. He suggests that the teacher taps on a diagram and the class call out the theorem (see his post for associated resources).
 |
| Chanting exercise from Don Steward |
Off on a tangent
I want to end with a couple of short non-syllabus ideas that would be nice to look at with your students if you have time.
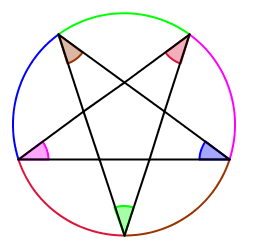
Have you ever looked at a regular pentagram? Aside from the symbolism in a number of cultures and an association with magic and mysticism, it has a number of interesting mathematical properties. It also makes a good discussion point when you teach circle theorems. This post has a neat and accessible proof of the sum of the vertex angles using the 'angle at the centre is twice the angle at circumference' theorem.
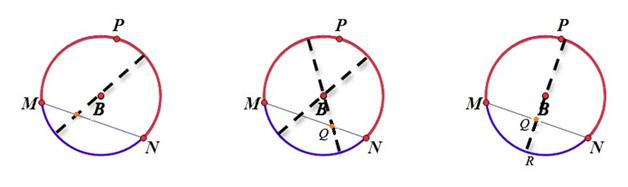
This post about Thales Theorem describes how the presenter of children's TV programme Art Attack demonstrated how to find the centre of a circle. If it featured on Art Attack then why not do it in a maths lesson? There is a nice interactive demonstration of the method here including printable instructions.
I want to end with a couple of short non-syllabus ideas that would be nice to look at with your students if you have time.
Have you ever looked at a regular pentagram? Aside from the symbolism in a number of cultures and an association with magic and mysticism, it has a number of interesting mathematical properties. It also makes a good discussion point when you teach circle theorems. This post has a neat and accessible proof of the sum of the vertex angles using the 'angle at the centre is twice the angle at circumference' theorem.
This post about Thales Theorem describes how the presenter of children's TV programme Art Attack demonstrated how to find the centre of a circle. If it featured on Art Attack then why not do it in a maths lesson? There is a nice interactive demonstration of the method here including printable instructions.
If you're teaching circle theorems for the first time or you just wanted some fresh ideas, I hope this post has been helpful. Please share your ideas and favourite resources in the comments below, or through Twitter.
This was a rather long post so if you made it this far and it's still November 2014, please vote for me in the UK Blog Awards! Thank you.
All O level material in this post was taken from Cambridge Assessment.






Here is a secondary school proof involving circle theorems:
ReplyDeletehttps://docs.google.com/document/d/1DlHM4C4D9Fvo4NsqNEpSukXCjoBx0XvIJyP0oX-BBIY/edit
Great stuff, thank you!
DeleteExcellent, as I'm about to teach this topic for the first time!
ReplyDeleteI love your ideas. Thank you.
ReplyDelete